前言

之前一直对“变分推断”这个词有一种恐惧的心理，听着就有点难懂，加上没学过泛函分析这块内容，潜意识里也很抵触”变分”，导致之前经常有选择性地忽略这一块知识点。如果你也一样和我有这样的心理，那么首先恭喜你称为了我的有缘人，其次再恭喜你看到了这篇博客，我尽可能从外行的角度通俗易懂地把”变分推断”展示出来，希望对有缘人有所启发。

我还是从为什么、是什么、怎么做三方面进行阐述。

为什么要用变分推断

一个算法的出现总是有问题驱动的，了解算法要解决的问题能帮助我们更好了解算法的用途。我们知道从贝叶斯角度来看待机器学习问题可以分为两个步骤：推断和决策。

说的通俗点推测就是先求参数的后验

$$p(\theta|X)$$

决策就是根据后验对测试数据进行预测

$$ p(x_{new}|X) = \int_{\theta} p(x_{new}|\theta) p (\theta|X) d \theta = E_{\theta|X}[p(x_{new}|\theta)] $$

也就相当于测试数据关于后验的期望。

但问题就在于这个后验的计算通常是非常困难的，对于不能精确推断 (直接计算)的后验分布，很朴素的想法就是近似推断，比如今天要讲的变分推断就属于确定性近似的一种方法；以及接下来还会再讲的随机近似，比如 MCMC。

第一个问题也就得到回答了，为什么要用变分推断？因为要计算后验分布的近似分布。

变分推断是什么

知道了为什么要用变分推断后，其实变分推断做的是什么也就顺理成章了，很朴素的想法就是用简单好搞的分布来逼近难求的后验分布。那怎么评价两个分布有多接近呢？那就看看这两个分布的 KL 散度 (这是非负的)，当 KL 散度为 0 时代表两个分布是一样的，因此变分推断要做的就是优化一个分布 $q(Z)$ 使得其与后验分布 $p(Z|X)$ 的 KL 散度最小化 (其中 $X$ 是观测数据，$Z$ 包含隐变量和参数)，用优化命题的形式来描述就是

$$ q^{*}(Z) = \arg \min_{q(Z)} \text{KL}(q(Z)||p(Z|X)) $$

但是 $p(Z|X)$ 本身就不知道的，这种直接求解的方式显然是行不通的，因此需要找个间接求解的方法。

根据贝叶斯公式有

$$ p(X) = \frac{p(X,Z)}{p(Z|X)} $$

两边取对数

$$ \ln p(X) = ln (p(X,Z)) - ln (p(Z|X)) $$

在推导 EM 算法时我们也是这么做的，先对上式右边加减一个关于 $Z$ 的分布 $q(Z)$，然后左边两边同时关于 $q(Z)$ 求期望。左边求期望还是等于本身 $\ln p(X)$，因此

$$ \begin{aligned} \ln p(X) &= \int_Z q(Z)\ln (\frac{p(X,Z)}{q(Z)}） dZ - \int_Zq(Z) \ln(\frac{p(Z|X)}{q(Z)}) dZ\\ &=\text{ELBO} + \text{KL}(q(Z)||p(Z|X)) \end{aligned} $$

为什么叫 ELBO？通常 $p(X)$ 称为 evidence，而 KL 散度是非负的，所以有

$$ \ln p(X) \ge \int_Z q(Z)\ln (\frac{p(X,Z)}{q(Z)}） dZ $$

因此不等式右边这项也就称为 evidence 的 lower bound (ELBO) 了。

我们之前想求的 KL 散度又出现了！虽然搞不定它，但是我们可以搞旁边的 ELBO 啊，刚才最小化 KL 散度不就转化为最大化 ELBO 了！再用优化命题的形式描述就是

$$ q(Z) = \arg \max_{q(Z)} \int_Z q(Z)\ln (p(X,Z)) dZ - \int_Z q(Z)\ln (q(Z)）dZ $$

因为 $q(Z)$ 是前面假设出来的关于 $Z$ 的分布，对这个分布还没有做任何假设，为了进一步推导便于求解，这里引入平均场理论，将 $q(Z)$ 划分为 $M$ 个相互独立的部分，即

$$ q(Z) = \prod_{i=1}^M q_i(Z_i) $$

采用如下的符号定义

$$ Z = \{Z_j,\bar{Z_j}\},\bar{Z_j} = Z \backslash Z_j $$

然后代入 ELBO 进行化简，我们一项一项来看

第一项为：

$$ \begin{aligned} &\int_Z q(Z)\ln (p(X,Z)) dZ\\ =&\int_{Z_1}...\int_{Z_M} \prod_{i=1}^M q_i(Z_i) \ln (p(X,Z)) dZ_1...dZ_M\\ =&\int_{Z_j}q_j(Z_j)[\int_{\bar{Z_j}}\prod_{i \not=j}^M q_i(Z_i) \ln(p(X,Z)) d \bar{Z_j}] d Z_j\\ =&\int_{Z_j}q_j(Z_j)E_{q(\bar{Z_j})} [\ln (p(X,Z))] d Z_j \end{aligned} $$

第二项为：

$$ \begin{aligned} &\int_Z q(Z)\ln (q(Z)）dZ\\ =&\int_{Z_1}...\int_{Z_M} \prod_{i=1}^M q_i(Z_i) \sum_{i=1}^M \ln (q_i(Z_i)) dZ_1...dZ_M\\ =&\sum_{i=1}^M\int_{Z_i} q_i(Z_i)\ln(q_i(Z_i))dZ_i\\ =&\int_{Z_j} q_j(Z_j)\ln(q_j(Z_j))dZ_j + C \end{aligned} $$

为了统一描述，定义

$$ \tilde{p}(X,Z_j) = E_{q(\bar{Z_j})} [\ln (p(X,Z))] $$

因此 ELBO 可以表示为

$$ \begin{aligned} \text{ELBO} &= \int_{Z_j}q_j(Z_j)E_{q(\bar{Z_j})} [\ln (p(X,Z))] d Z_j - \int_{Z_j} q_j(Z_j)\ln(q_j(Z_j))dZ_j - C\\ &=\int_{Z_j} q_j(Z_j)\ln\frac{\tilde{p}(X,Z_j)}{q_j(Z_j)}dZ_j - C\\ &=-\text{KL}(q_j(Z_j)||\tilde{p}(X,Z_j)) - C \end{aligned} $$

也就是将 ELBO 转化成另外一个 KL 散度，ELBO取最大值时对应 KL 散度取等号，即

$$ q_j^{*}(Z_j) = \tilde{p}(X,Z_j) $$

将 $\tilde{p}(X,Z_j)$ 的定义代入得

$$ \ln (q_j^{*}(Z_j)) = E_{q(\bar{Z_j})} [\ln (p(X,Z))] $$

通俗来说就是用对数联合概率分布关于利用除了 $Z_j$ 以外的其他分布的期望来更新 $Z_j$ 的分布。这是一个迭代的过程：

$$ \begin{aligned} \ln(q_1^{*}(Z_1)) &= \int_{Z_2} \int_{Z_3}... \int_{Z_M} q_2({Z_2})...q_M(z_M)\ln (p(X,Z)) dZ_2d Z_3 ... dZ_M\\ \ln(q_2^{*}(Z_2)) &= \int_{Z_1^*} \int_{Z_3}... \int_{Z_M} q_1^*({Z_1}) q_2({Z_3})...q_M(z_M) \ln (p(X,Z)) dZ_1^* dZ_3 ... dZ_M\\ &...\\ \ln(q_M^{*}(Z_M)) &= \int_{Z_1^*} \int_{Z_2^*}... \int_{Z_{M-1}} q_1^*({Z_1})...q_{M-1}^*(z_{M-1}) \ln (p(X,Z)) dZ_1^* dZ_2^* ... dZ_{M-1}^* \end{aligned} $$

迭代收敛得到的分布 $q(Z)$ 就是要求的后验分布的 $p(Z|X)$ 的近似分布了。

变分推断怎么用

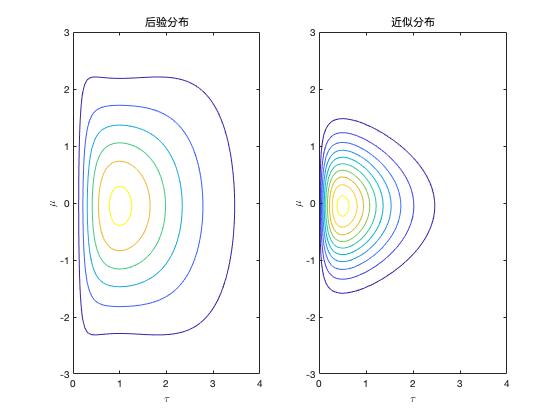
知道了变分推断是怎么一回事后，更多人想要知道具体使用时是怎么用的，这里用一个一元高斯分布的例子进行说明，该例子选自《徐亦达机器学习》系列。结合 matlab 代码跟我一起来实现一下变分推断吧

首先假设你有个数据集 $D =$ {$x_1,…,x_N$} 来自一个高斯分布 $\mathcal{N}(0,1)$，这个均值和方差我们是不知道的，也就是等下要从数据中去学习的 $p(\mu,\tau|D)$，其中 $\tau=1/\sigma^2$。

1
2
3
4

N = 100;
mu_0 = 0; 
sigma_0 = 1;
D = mu_0 + sigma_0* randn(N,1);

根据贝叶斯公式我们有

$$ p(\mu,\tau|D) \propto p(D|\mu,\tau)p(\mu|\tau)p(\tau) $$

因此要学习参数的分布，需要先对参数假定一个先验，因为 $\tau$ 大于 0 的性质，假设其为 Gamma 分布 $Gamma(\tau|a_0,b_0)$，$p(\mu|\tau)$ 为高斯分布 $\mathcal{N}(\mu_0,(\lambda_0 \tau)^{-1})$，由于共轭性可以直接得到后验分布的解析形式

$$ p(\mu,\tau|D) = \mathcal{N}(\mu_n,(\lambda_n\tau)^{-1})Gamma(\tau|a_n,b_n) $$

且参数 $\mu_n,\lambda_n,a_n,b_n$ 直接可以得到

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

% 先验分布里的参数
lambda_0 = 1;
a_0 = 1.5;
b_0 = 1;

% 后验分布的参数 
mu_n = (lambda_0 * mu_0 + N * mean(D) )/ (lambda_0 + N);
lambda_n = lambda_0 + N;
a_n = a_0 + N/2;
b_n = b_0 + 1/2 * sum((X - mean(X)).^2) + (lambda_0*n * (mean(X) - mu_0)^2)/(2*(lambda_0 + N));

但是我们要假装不知道这个共轭分布能直接这么得到，用变分推断来求求看，首先假设 $q(Z)$ 由独立的两部分组成，在这里就是

$$ q(\mu,\tau) = q_{\mu}(\mu)q_{\tau}(\tau) $$

根据之前推导得到的变分推断的迭代公式对应为

$$ \begin{aligned} \ln(q_{\mu}^{*}(\mu)) &= \int_{\tau} q_{\tau}(\tau) \ln (p(X,Z)) d \tau\\ \ln(q_{\tau}^{*}(\tau)) &= \int_{\mu^*} q_{\mu}^*(\mu) \ln (p(X,Z)) d \mu^* \end{aligned} $$

化简为

$$ \begin{aligned} \ln \left(q_{\mu}^{*}(\mu)\right) &=-\frac{E_{q_{\tau}}[\tau]}{2}\left[\sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}+\lambda_{0}\left(\mu-\mu_{0}\right)^{2}\right]+\text { const } \\ &=-\frac{E_{q_{\tau}}[\tau]\left(n+\lambda_{0}\right)}{2}\left(\mu-\frac{\left(N \overline{x}+\lambda_{0} \mu_{0}\right)}{\left(N+\lambda_{0}\right)}\right)^{2}+\text { const } \\ &=\mathcal{N}\left(\frac{N \overline{x}+\lambda_{0} \mu_{0}}{N+\lambda_{0}}, E_{q_{\tau}}[\tau]\left(N+\lambda_{0}\right)\right) \end{aligned} $$
1
2
3

E_tau = a_current/b_current; % Gamma分布的均值
mu_current       = (lambda_0 * mu_0 + N * mean(X))/(lambda_0 + N);
lambda_current   = (lambda_0 + N) * E_tau;
$$ \ln {q^*_{\tau}(\tau)}=(\underbrace{\frac{N}{2}+a_{0}-1}_{a_{n}}) \ln (\tau)-\tau(\underbrace{b_{0}+\frac{1}{2} E_{q_{\mu}^*(\mu)}\left[\sum_{i=1}^{N}\left(x_{i}-\mu\right)^{2}+\lambda_{0}\left(\mu-\mu_{0}\right)^{2}\right]}_{b_{n}})+\text { const } $$ 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10

a_current  = a_0 + N/2;
% E[mu^2] = var(mu) + (E[mu])^2
E_mu_square = inv(lambda_0) + mu_prev^2;
% E[mu]
E_mu = mu_prev;
%sum [(x_i - mu)^2]
first = sum( X.^2 - 2 * X .* repmat(E_mu,size(X)) + repmat(E_mu_square, size(X)));
%lambda_0 (mu - mu_0)^2
second = lambda_0 *(E_mu_square - 2*mu_0*E_mu + mu_0^2);
b_current = b_0 + (first + second)/2;

根据两个分布不断迭代就能得到最终两个分布各自的参数，然后两个分布的乘积就是要求的后验分布的近似分布了。

总结

当我们遇到难搞的后验分布时，可以用容易表达和求解的分布来近似，常规的变分推断基于平均场理论，假设近似分布由独立的几部分组成，通过最大化 ELBO 我们可以得到近似分布各个独立部分的迭代求解式，可以理解为积分(求期望)掉 $Z_j$ 外的其他部分得到 $Z_j$ 的更新，类似坐标上升法的思想，先固定其它然后求其中一项。

基于平均场理论的变分推断假设(要求各部分独立)还是比较强的，比如上面的例子中 $\mu$ 和 $\tau$ 其实并不是独立的，$p(\mu/\tau)$ 是个高斯分布；其次这种递推求解的方式中还是涉及了许多的积分，计算量大。因此改进的方法还有随机梯度变分推断，感兴趣的可以看看shuhuai大神的讲解。