前面总结了 EM 算法，我们知道这是一个采用迭代的方式用于解决含有隐变量的参数估计问题的算法。典型的一个应用就是今天的主角高斯混合模型 (Gaussian Misture Model)。这个模型和它的名字一样直白，也就是由多个高斯分布组合而成的模型，其概率密度函数可以表示为

$$ p(x) = \sum_{k=1}^K \alpha_k \cdot \mathcal{N}(x|\mu_k,\Sigma_k) $$

这不就是 $K$ 个单高斯模型 $\mathcal{N}(x|\mu_k,\Sigma_k),k=1,…,K$ 加权而成，$\alpha_k$ 则是对应单高斯模型的权重，且满足 $\sum_{k=1}^K \alpha_k = 1$。这样做很直观的原因是混合多个单一模型得到复杂模型自然能够生成更复杂的样本，并且理论上如果 $K$ 足够大且权重合理，得到的混合模型能够拟合任意分布。

模型参数学习

对混合高斯模型，我们要确定的参数有单高斯的个数 $K$ (你要混合几个单高斯总要告诉模型吧，通常直接给定或者采用一定的评价指标来确定合适的 $K$ 值)，每个单高斯分布的均值 $\mu_k$ 和方差 $\Sigma_k$ 以及对应的权重 $\alpha_k$。也就是我们需要从观测数据 $x_1,…,x_N$ 中学习得到这些模型参数。

对于每一个样本 $x$，从生成模型的角度来理解：以 $\alpha_k$ 的概率选择第 $k$ 个高斯元 $\mathcal{N}(x|\mu_k,\Sigma_k)$，然后进行采样。

但是观测数据 $x_1,…,x_N$ 并没有告诉我们每一个样本采样自哪一个单高斯分布，因此引入隐变量 $z$，其分布满足

$z$ 1 2 … $K$
$p(z)$ $p_1$ $p_2$ … $p_K$

如果 $z_i = 1$ 表示第 $i$ 个样本 $x_i$ 采样自第 1 个单高斯分布，概率为 $p_1$ (也就相当于前面说的权重 $\alpha_1$)。

定义完隐变量后，对于任意样本，完整数据 (观测数据和隐变量) 的概率密度函数可以表示为

$$ p(x,z) = p(z)p(x|z) = p(z) \mathcal{N}(x|\mu_z,\Sigma_z) $$

假设各个样本之间相互独立，则观测数据的似然函数可以表示为

$$ L(\theta) = \prod_{i=1}^N p(x_i|\theta) = \prod_{i=1}^N \int_{z_i} p(x_i,z_i|\theta) dz_i = \prod_{i=1}^N \sum_{k=1}^K p_k \mathcal{N}(x_i | \mu_k,\Sigma_k) $$

上式中，观测数据的概率分布通过对完整数据的概率分布进行积分操作消除隐变量，对于离散变量 $z$ 也就是转化为求和操作。

对数似然函数为

$$ \ln L(\theta) = \sum_{i=1}^N \ln \sum_{k=1}^K p_k \mathcal{N}(x_i | \mu_k,\Sigma_k) $$

如果要像往常一样采用求导的方式来估计参数行不通了，因为对数里面还有求和。所以就要用 EM 算法来迭代求解啦。

EM 算法与 GMM

这里直接给出参数估计的迭代公式(不清楚的可以翻翻前面关于 EM 算法的博客)

$$ \theta^{(t+1)} = \arg \max_{\theta} Q(\theta,\theta^{(t)}) = \arg \max_{\theta} E_{Z|X,\theta^{(t)}}[\log p(X,Z|\theta)] $$

即需要先求隐变量 $Z$ 的后验，然后再令期望 $Q(\theta,\theta^{(t)})$ 最大化。

进一步可以表示为

$$ \begin{aligned} Q(\theta,\theta^{(t)}) &= \int_Z \log p(X,Z|\theta) p(Z|X,\theta^{(t)}) dZ\\ &=\sum_{z_1,...,z_N} \log \prod_{i=1}^N p(x_i,z_i|\theta) \prod_{i=1}^N p(z_i|x_i,\theta^{(t)})\\ &=\sum_{z_1,...,z_N} (\sum_{i=1}^N \log p(x_i,z_i|\theta)) \prod_{i=1}^N p(z_i|x_i,\theta^{(t)})\\ &=\sum_{z_1,...,z_N} \log p(x_1,z_1|\theta) p(z_1|x_1,\theta^{(t)}) \prod_{i=2}^N p(z_i|x_i,\theta^{(t)})\\ &+ ... + \sum_{z_1,...,z_N} \log p(x_N,z_N|\theta) p(z_N|x_N,\theta^{(t)}) \prod_{i=1}^{N-1} p(z_i|x_i,\theta^{(t)})\\ &=\sum_{i=1}^N \sum_{z_i} \log p(x_i,z_i|\theta)p(z_i|x_i,\theta^{(t)})\\ &=\sum_{i=1}^N \sum_{k=1}^K \log p(x_i,z_i=k|\theta)p(z_i=k|x_i,\theta^{(t)}) \end{aligned} $$

其中隐变量的后验分布为

$$ \begin{aligned} p(z_i=k|x_i,\theta^{(t)}) &= \frac {p(z_i=k,x_i|\theta^{(t)})}{p(x_i|\theta^{(t)})}\\ &=\frac{p^{(t)}_k \mathcal{N}(x_i|\mu^{(t)}_k,\Sigma^{(t)}_k)}{\sum_{k=1}^K p^{(t)}_k \mathcal{N}(x_i|\mu^{(t)}_k,\Sigma^{(t)}_k)} \end{aligned} $$

联合分布为

$$ \log p(x_i,z_i=k|\theta) = \log p_k + \log \mathcal{N}(x_i|\mu_k,\Sigma_k) $$

即

$$ Q(\theta,\theta^{(t)})=\sum_{k=1}^K\sum_{i=1}^N [\log p_k +\log \mathcal{N}(x_i|\mu_k,\Sigma_k)]p(z_i=k|x_i,\theta^{(t)}) $$

记住这里 $p(z_i=k|x_i,\theta^{(t)})$ 相当于是个常数，然后根据最大化期望函数 $Q(\theta,\theta^{(t)})$ 的原则依次求解 $p_k,u_k,\Sigma_k$，由于 $p_k$ 额外满足等式约束 $\sum_{k=1}^K p_k=1$，求解 $p_k$ 是一个带有等式约束的最大化问题需要用到拉格朗日乘子法(不清楚的也可以翻翻之前的文章)，$u_k,\Sigma_k$ 则直接对期望函数求导利用极值条件就能得到解析解。

对于参数 $p_k$，拉格朗日函数可以表示为：

$$ \mathcal{L}(p_k,\lambda) = \sum_{k=1}^K\sum_{i=1}^N \log p_k p(z_i=k|x_i,\theta^{(t)}) + \lambda(\sum_{k=1}^K p_k - 1) $$

令 $\partial \mathcal{L}/\partial p_k=0$

$$ \begin{aligned} \sum_{i=1}^N \frac{1}{p_k}p(z_i=k|x_i,\theta^{(t)}) + \lambda = 0\\ \sum_{i=1}^N p(z_i=k|x_i,\theta^{(t)}) + p_k \lambda = 0\\ \sum_{k=1}^K\sum_{i=1}^N p(z_i=k|x_i,\theta^{(t)}) + \lambda = 0\\ \sum_{i=1}^N \sum_{k=1}^K p(z_i=k|x_i,\theta^{(t)}) + \lambda = 0\\ N+\lambda = 0 \end{aligned} $$

第三式到第四式利用 $\sum_{k=1}^K p_k = 1$，第三式到第四式利用离散随机变量的概率密度函数对所有可能情况求和为1，然后将最后一式代入第一式可得

$$ p_k^{(t+1)} = \frac{1}{N} \sum_{i=1}^N p(z_i=k|x_i,\theta^{(t)}) $$

对于参数 $u_k$，直接对 $Q$ 函数求导，并令 $\partial Q/ \partial u_k=0$:

$$ \begin{aligned} \frac{\partial}{\partial u_k} \sum_{k=1}^K \sum_{i=1}^N \log [\frac{1}{{(2\pi)}^{(d/2)}|\Sigma_k|^{(1/2)}}\exp(-\frac{1}{2} (x_i - u_k)^T \Sigma_k^{(-1)}(x_i -u_k) )]p(z_i=k|x_i,\theta^{(t})=0\\ \frac{\partial}{\partial u_k} \sum_{k=1}^K \sum_{i=1}^N [-\frac{d}{2} \log 2\pi -\frac{1}{2} \log|\Sigma_k| -\frac{1}{2} (x_i - u_k)^T \Sigma_k^{(-1)}(x_i -u_k)] p(z_i=k|x_i,\theta^{(t)})=0\\ \sum_{i=1}^N (x_i-u_k)^T\Sigma_k^{(-1)} p(z_i=k|x_i,\theta^{(t)})=0 \end{aligned} $$

根据最后一式可得：

$$ u_k^{(t+1)} = \frac{\sum_{i=1}^Nx_i p(z_i=k|x_i,\theta^{(t)})}{\sum_{i=1}^N p(z_i=k|x_i,\theta^{(t)})} $$

对于参数 $\Sigma_k$，直接对 $Q$ 函数求导，并令 $\partial Q/ \partial \Sigma_k=0$:

$$ \begin{aligned} \frac{\partial}{\partial \Sigma_k} \sum_{k=1}^K \sum_{i=1}^N \log [\frac{1}{{(2\pi)}^{(d/2)}|\Sigma_k|^{(1/2)}}\exp(-\frac{1}{2} (x_i - u_k)^T \Sigma_k^{(-1)}(x_i -u_k) )]p(z_i=k|x_i,\theta^{(t})=0\\ \frac{\partial}{\partial \Sigma_k} \sum_{k=1}^K \sum_{i=1}^N [-\frac{d}{2} \log 2\pi -\frac{1}{2} \log |\Sigma_k| -\frac{1}{2} (x_i - u_k)^T \Sigma_k^{(-1)}(x_i -u_k)] p(z_i=k|x_i,\theta^{(t)})=0\\ \sum_{i=1}^N [-\frac{1}{2}(\Sigma_k^{(-1)})^T + \frac{1}{2} \Sigma_k^{(-1)}(x_i-u_k) (x_i-u_k)^T \Sigma_k^{(-1)}]p(z_i=k|x_i,\theta^{(t)})=0\\ \sum_{i=1}^N [-\Sigma_k + (x_i - u_k)(x_i - u_k)^T] p(z_i=k|x_i,\theta^{(t)})=0\\ \end{aligned} $$

根据最后一式可得：

$$ {\Sigma_k}^{(t+1)} = \frac{\sum_{i=1}^N (x_i - u_k)(x_i - u_k)^T p(z_i=k|x_i,\theta^{(t)})}{\sum_{i=1}^N p(z_i=k|x_i,\theta^{(t)})} $$

matlab实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77

clear
clear all;
% 生成数据 由3个二元高斯分布各生成1000个样本
mu1 = [1 2];
Sigma1 = [2 0;0 0.5];
mu2 = [-3 -5];
Sigma2 = [1 0;0 1];
mu3 = [2 -3];
Sigma3 = [1 0;0 2];
rng(1); % For reproducibility
X = [mvnrnd(mu1,Sigma1,1000);mvnrnd(mu2,Sigma2,1000);mvnrnd(mu3,Sigma3,1000)];
[N, d] = size(X); % 样本数、样本维度
figure
y = [0*ones(1000,1);ones(1000,1);2*ones(1000,1)];
h = gscatter(X(:,1),X(:,2),y);
legend(h,'Gaussian 1','Gaussian 2','Gaussian 3')

% 初始参数
K     = 3; % 单高斯的个数
p_k   = ones(K,1)*1/K; % 各个高斯元的权重系数
mu    = rand(K, d); % 待估计的均值，每一行是一个高斯分布的均值
sigma = zeros(d, d, K); % 待估计的协方差矩阵
for k = 1:K
    sigma(:, :, k) = eye(d);
end

% 概率密度函数表达式
pdf_value = @(x,mu,Sigma) 1/((2*pi)^(d/2)*(det(Sigma))^(1/2))*exp(-0.5*(x-mu)*inv(Sigma)*(x-mu)');

% EM算法估计参数
p_z = repmat(ones(1,K)*1/K,N,1); % 隐变量的后验分布矩阵，每一个样本对应K个后验

% 迭代1000次，可以自己设置各种结束迭代条件
for iter = 1:1000
    % E 步 计算后验
    for i = 1:N
        p_xi = 0; % 后验的分母p(x_i|theta^(t))
        for j = 1:K
            p_xi = p_xi + p_k(j)*pdf_value(X(i,:),mu(j,:),sigma(:,:,j));
        end
        for k = 1:K
            p_z(i,k) = p_k(k)*pdf_value(X(i,:),mu(k,:),sigma(:,:,k))/p_xi;
        end
    end

    % M 步
    for k = 1:K
        p_k(k)  = 1/N*sum(p_z(:,k)); % 更新权重
        num = 0; % 均值的分子
        for i = 1:N
            num = num + X(i,:)*p_z(i,k);
        end
        mu(k,:) = num/sum(p_z(:,k)); % 更新均值
    end
    
    for k = 1:K
        num = 0; % 协方差的分子
        for i = 1:N
            num = num + (X(i,:)-mu(k,:))'*(X(i,:)-mu(k,:))*p_z(i,k);
        end
        sigma(:,:,k) = num/sum(p_z(:,k)); % 更新协方差
    end
end

% 画各个高斯分布的等高线
for k = 1:K
    x1 = -7:.2:7;
    x2 = -9:.2:5;
    [X1,X2] = meshgrid(x1,x2);
    X = [X1(:) X2(:)];
    y = mvnpdf(X,mu(k,:),sigma(:,:,k));
    y = reshape(y,length(x2),length(x1));
    hold on 
    contour(x1,x2,y,[0.0001 0.001 0.01 0.05 0.15 0.25 0.35])
    xlabel('x_1')
    ylabel('x_2')
end

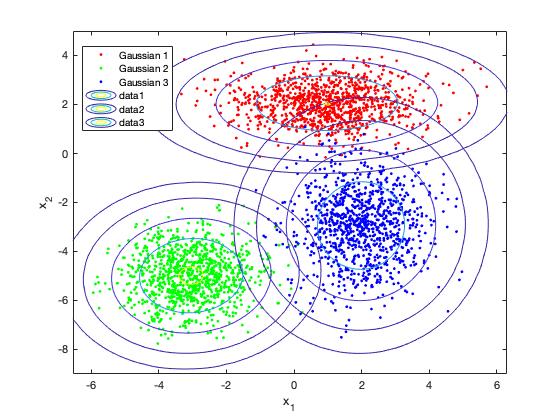
散点就是由三个不同的高斯分布生成的样本，等高线则是根据学习出来的三个高斯元画的。