「机器学习」高斯过程
网上机器学习的算法铺天盖地,高斯过程却显得不那么起眼,它与其他大多数算法不一样的地方在于,它提供了不确定性的估计,这篇文章争取在不涉及数学推导的情况下给大家一个直观的理解。
什么是不确定性?
我觉得最能代表不确定性的应该就是概率分布(probability distribution)了,不了解概率分布也没关系,骰子摇过吧,一个六面均匀的骰子,摇到任一数字的概率是多少?答案是显然的: $\frac{1}{6}$,这就是一个离散的概率分布,有六种可能的结果(朝上的面为1、2、3、4、5或6),每种结果的可能性为 $\frac{1}{6}$。进一步延伸一下,离散概率分布的升级版就是连续概率分布,它的可能结果可就不是简单几种情况那么简单了,可以是任意实数,比如人的身高,中国男性的身高统计出来画一下,你就能看到一个中间高两边低的正态分布的样子了。
那么已知概率分布后,如何采样呢?很简单呀,比如骰子你摇一次就是从这个离散概率分布中采样一次。
贝叶斯推断
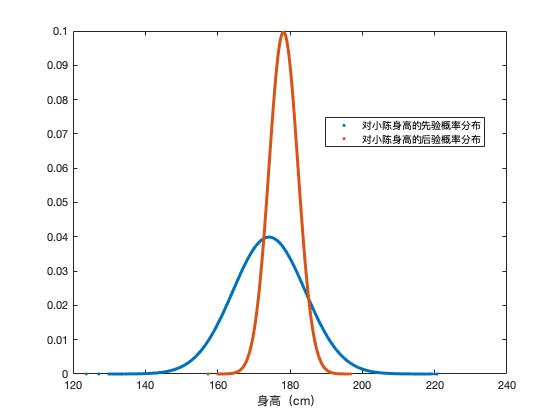
一提到贝叶斯推断,可能要吓跑一群人,别跑!等我给你介绍完就不怕了! 其实贝叶斯推断就是根据我们观察到的现象去更新我们脑袋里的认知。再具体点就是:我们在事情没发生前对这件事情有所认知(或者叫做先验),通常可以用一个概率分布来表示,然后在得到一些发生的事实后,我们会对这件事情的认知有所该表(就是得到了后验);而把这些东西联系到一起的就是大名鼎鼎的贝叶斯定理。
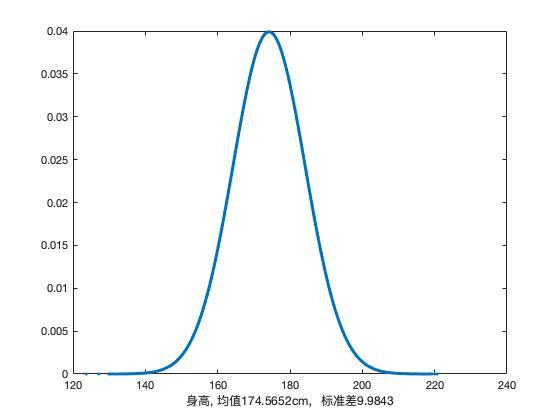
还是不够形象?那我们来个例子,上面说过离散概率分布了,这次我们来个连续的看看,来看看身高吧,来猜猜小陈有多高(猜对有奖哦,文末二维码随意扫随意打赏哈),你又不认识我没见过我,怎么知道我有多高呢,那直观的猜测就是小陈是个中国人,小陈的身高服从中国人身高的概率分布(假设你能得到这个概率分布咯)
什么是高斯过程?
好了,今天的主角登场了,高斯过程其实就是函数的概率分布,既然是概率分布,再用上面贝叶斯的套路我们就也能够通过训练数据来更新它的概率分布。
我们来理一下思路,函数是什么,最简单的回顾你初中学的 $y=f(x)$ 就是个函数(随便函数形式都行,一次二次正弦等等),把它画一下就是在 XY 平面上的一条线呗;既然是概率分布还是高斯的,那总有均值吧,总有协方差吧,在这里对应就是均值函数和协方差函数。因此高斯过程本质就是由均值函数和协方差函数决定的一个随机过程。
比如有一个sin函数,我们有五个点的训练数据

1 2 3 |
Xtrain = np.array([-3, -2, -1, 1, 2]).reshape(5,1) ytrain = np.sin(Xtrain) pl.plot(Xtrain, ytrain, 'bs', ms=8) |
没有训练前我们对这个函数没什么认知,那就假设其均值函数为0(大部分时候也都是当做0来使用的),核函数就取SE核函数吧(这个是什么先不管啦,你就认为是个用来生成协方差矩阵的函数,主要我们是要得到它的协方差呀!核函数里一般会有超参数需要估计,为了简单起见,我直接直接给定超参数,不去估计这个参数了),在这样的先验分布下,你得到的函数会是什么样的呢?我们从这个函数的概率分布中采样三个函数出来看看。
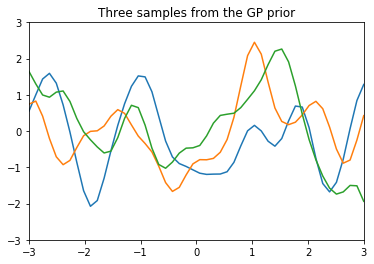
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 |
import numpy as np
import matplotlib.pyplot as pl
%matplotlib inline
# Test data
n = 50
Xtest = np.linspace(-3, 3, n).reshape(-1,1)
# Define the kernel function
def kernel(a, b, param):
sqdist = np.sum(a**2,1).reshape(-1,1) + np.sum(b**2,1) - 2*np.dot(a, b.T)
return np.exp(-.5 * (1/param) * sqdist)
param = 0.1
K_ss = kernel(Xtest, Xtest, param)
# Get cholesky decomposition (square root) of the
# covariance matrix
L = np.linalg.cholesky(K_ss + 1e-15*np.eye(n))
# Sample 3 sets of standard normals for our test points,
# multiply them by the square root of the covariance matrix
f_prior = np.dot(L, np.random.normal(size=(n,3)))
# Now let's plot the 3 sampled functions.
pl.plot(Xtest, f_prior)
pl.axis([-3, 3, -3, 3])
pl.title('Three samples from the GP prior')
pl.show() |
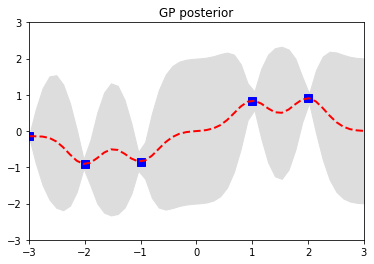
那再根据训练数据训练一发,也就是相当于前面提到的贝叶斯推断,就能得到函数的后验概率分布
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
# Apply the kernel function to our training points
K = kernel(Xtrain, Xtrain, param)
L = np.linalg.cholesky(K + 0.00005*np.eye(len(Xtrain)))
# Compute the mean at our test points.
K_s = kernel(Xtrain, Xtest, param)
Lk = np.linalg.solve(L, K_s)
mu = np.dot(Lk.T, np.linalg.solve(L, ytrain)).reshape((n,))
# Compute the standard deviation so we can plot it
s2 = np.diag(K_ss) - np.sum(Lk**2, axis=0)
stdv = np.sqrt(s2)
# Draw samples from the posterior at our test points.
L = np.linalg.cholesky(K_ss + 1e-6*np.eye(n) - np.dot(Lk.T, Lk))
f_post = mu.reshape(-1,1) + np.dot(L, np.random.normal(size=(n,3)))
pl.plot(Xtrain, ytrain, 'bs', ms=8)
pl.gca().fill_between(Xtest.flat, mu-2*stdv, mu+2*stdv, color="#dddddd")
pl.plot(Xtest, mu, 'r--', lw=2)
pl.axis([-3, 3, -3, 3])
pl.title('GP posterior')
pl.show() |
这个回归效果很差,主要因为核函数的超参数没估计,而且训练的数据太少了。感兴趣可以自己去改改代码试试看。详细的推导和理论可以看06年的那本《Gaussian Process for Machine Learning》
划重点
先验 “加” 数据得到后验;后验”加权平均”输出就是预测!
最后的最后上两个公式吧